欧拉公式，世界上最完美的公式

欧拉公式是什么？为什么欧拉公式被称为世界上最完美的公式？下面我们就一起来了解一下吧。
欧拉公式又称为欧拉定理，也称为尤拉公式，是用在复分析领域的公式，欧拉公式将三角函数与复数指数函数相关联，之所以叫作欧拉公式，那是因为欧拉公式是由莱昂哈德·欧拉提出来的，所以用他的名字进行了命名。
尤拉公式提出，对任意实数 x，都存在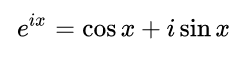

其中 e是自然对数的底数， i是虚数单位，而  \cos和  \sin则是余弦、正弦对应的三角函数，参数 x则以弧度为单位。这一复数指数函数有时还写作 {cis}(x)（英语：cosine plus i sine，余弦加i正弦）。由于该公式在 x为复数时仍然成立，所以也有人将这一更通用的版本称为尤拉公式。

莱昂哈德·欧拉出生于1707年4月15日，死于公元1783年9月18日，莱昂哈德·欧拉是一位来自于瑞士的数学家和物理学家，是近代著名的数学家之一，此外，莱昂哈德·欧拉还有力学，光学和天文学上都作出了重大的贡献。

莱昂哈德·欧拉被认为是18世纪，世界上最杰出的数学家，也是史上最伟大的数学家之一，而且莱昂哈德·欧拉还有许多的著作，他的学术著作就多达60-80册。
他对微分方程理论作出了重要贡献。他还是欧拉近似法的创始人，这些计算法被用于计算力学中。此中最有名的被称为欧拉方法。

在数论里他引入了欧拉函数。自然数  n的欧拉函数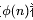被定义为小于n并且与 n互质的自然数的个数。

在计算机领域中广泛使用的RSA公钥密码算法也正是以欧拉函数为基础的。

在分析领域，是欧拉综合了戈特弗里德·威廉·莱布尼茨的微分与艾萨克·牛顿的流数。

他在1735年由于解决了长期悬而未决的贝塞尔问题而获得名声：

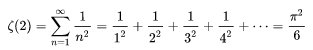
其中是黎曼函数。

欧拉将虚数的幂定义为如下公式

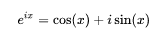
这就是欧拉公式，它成为指数函数的中心。在初等分析中，从本质上来说，要么是指数函数的变种，要么是多项式，两者必居其一。被理查德·费曼称为“最卓越的数学公式”的则是欧拉公式的一个简单推论（通常被称为欧拉恒等式）：

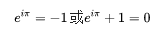
他在1735年定义了微分方程中的欧拉-马斯刻若尼常数，也是欧拉-麦克劳林求和公式的发现者之一，这一公式在计算难于计算的积分、求和与级数的时候极为有效：

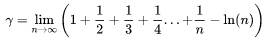
欧拉还发现了公式的 V - e + f = 2 的数量与顶点(Vertex, V)，边(edge, e)和面(face, f)的凸多面体，因此，对一个平面图形。此公式中的常数是现在被称为欧拉示性数的图形（或其他数学对象），是有关属的对象。研究和推广这一公式，特别是通过柯西和欧莱雅Huillier，是在原点的拓扑结构。

2013年4月15日Google以doodle纪念欧拉306周年诞辰，展示了欧拉角、欧拉公式、欧拉恒等式、欧拉示性数和七桥问题等。

为什么欧拉公式被称为世界上最完美的公式了？

欧拉公式的巧妙之处在于，它没有任何多余的内容，将数学中最基本的e、i、π放在了同一个式子中，同时加入了数学也是哲学中最重要的0和1，再以简单的加号相连。高斯曾经说：“一个人第一次看到这个公式而不感到它的魅力，他不可能成为数学家。” 虽然不敢肯定她是世界上“最伟大公式"，但是可以肯定它是最完美的数学公式之一。

理由如下：

1、自然数的“e”含于其中。 自然对数的底，大到飞船的速度，小至蜗牛的螺线，谁能够离开它？

2、最重要的常数 π 含于其中。 世界上最完美的平面对称图形是圆。“最伟大的公式”能够离开圆周率吗？ (还有π和e是两个最重要的无理数！)

3、最重要的运算符号 + 含于其中。 之所以说加号是最重要的符号，是因为其余符号都是由加号派生而来。减号是加法的逆逆运算，乘法是累计的加法……

4、最重要的关系符号 = 含于其中。 从你一开始学算术，最先遇见它，相信你也会同意这句话。

5、最重要的两个元在里面。零元0 ，单位1 ，是构造群，环，域的基本元素。如果你看了有关《近世代数》的书，你就会体会到它的重要性。

6、最重要的虚单位 i 也在其中。 虚单位 i 使数轴上的问题扩展到了平面，而在哈密尔的 4 元数与 凯莱的 8 元数中也离开不了它。 之所以说她美，是因为这个公式的精简。她没有多余的字符，却联系着几乎所有的数学知识。 有了加号，可以得到其余运算符号； 有了0，1，就可以得到其他的数字； 有了 π 就有了圆函数，也就是三角函数； 有了 i 就有了虚数，平面向量与其对应，也就有了哈密尔的 4 元数，现实的空间与其对应； 有了 e 就有了微积分，就有了和工业革命时期相适宜的数学。

三角形中的欧拉公式： 设r为三角形外接圆半径，r为内切圆半径，d为外心到内心的距离，则： d＾2=r＾2-2rr

拓扑学里的欧拉公式： v+f-e=x(p)，v是多面体p的顶点个数，f是多面体p的面数，e是多面体p的棱的条数,x(p)是多面体p的欧拉示性数。 如果p可以同胚于一个球面（可以通俗地理解为能吹胀而绷在一个球面上），那么x(p)=2，如果p同胚于一个接有h个环柄的球面，那么x(p)=2-2h。 x(p)叫做p的欧拉示性数，是拓扑不变量，就是无论再怎么经过拓扑变形也不会改变的量，是拓扑学研究的范围。

在多面体中的运用: 简单多面体的顶点数v、面数f及棱数e间有关系 v+f-e=2 这个公式叫欧拉公式。公式描述了简单多面体顶点数、面数、棱数特有的规律。

初等数论里的欧拉公式： 欧拉φ函数：φ(n)是所有小于n的正整数里，和n互素的整数的个数。n是一个正整数。 欧拉证明了下面这个式子： 如果n的标准素因子分解式是p1^a1*p2^a2*……*pm^am，其中众pj(j=1,2,……,m)都是素数，而且两两不等。则有 φ(n)=n(1-1/p1)(1-1/p2)……(1-1/pm) 利用容斥原理可以证明它。 此外还有很多著名定理都以欧拉的名字命名。